Definition and Mathematics of Work
In the first three units of The Physics Classroom, we utilized Newton's laws to analyze the motion of objects. Force and mass information were used to determine the acceleration of an object. Acceleration information was subsequently used to determine information about the velocity or displacement of an object after a given period 
of time. In this manner, Newton's laws serve as a useful model for analyzing motion and making predictions about the final state of an object's motion. In this unit, an entirely different model will be used to analyze the motion of objects. Motion will be approached from the perspective of work and energy. The effect that work has upon the energy of an object (or system of objects) will be investigated; the resulting velocity and/or height of the object can then be predicted from energy information. In order to understand this work-energy approach to the analysis of motion, it is important to first have a solid understanding of a few basic terms. Thus, Lesson 1 of this unit will focus on the definitions and meanings of such terms as work, mechanical energy, potential energy, kinetic energy, and power.
When a force acts upon an object to cause a displacement of the object, it is said that work was done upon the object. There are three key ingredients to work - force, displacement, and cause. In order for a force to qualify as having done work on an object, there must be a displacement and the force must cause the displacement. There are several good examples of work that can be observed in everyday life - a horse pulling a plow through the field, a father pushing a grocery cart down the aisle of a grocery store, a freshman lifting a backpack full of books upon her shoulder, a weightlifter lifting a barbell above his head, an Olympian launching the shot-put, etc. In each case described here there is a force exerted upon an object to cause that object to be displaced. Mathematically, work can be expressed by the following equation. where F is the force, d is the displacement, and the angle (theta) is defined as the angle between the force and the displacement vector. Perhaps the most difficult aspect of the above equation is the angle "theta." The angle is not just any 'ole angle, but rather a very specific angle. The angle measure is defined as the angle between the force and the displacement. To gather an idea of it's meaning, consider the following three scenarios. It can be accurately noted that the waiter's hand did push forward on the tray for a brief period of time to accelerate it from rest to a final walking speed. But once up to speed, the tray will stay in its straight-line motion at a constant speed without a forward force. And if the only force exerted upon the tray during the constant speed stage of its motion is upward, then no work is done upon the tray. Again, a vertical force does not do work on a horizontally displaced object.
Work Equation
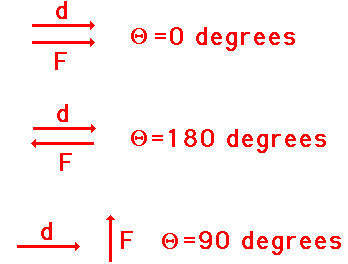
To Do Work, Forces Must Cause Displacements
Let's consider Scenario C above in more detail. Scenario C involves a situation similar to the waiter who carried a tray full of meals above his head by one arm straight across the room at constant speed. It was mentioned earlier that the waiter does not do work upon the tray as he carries it across the room. The force supplied by the waiter on the tray is an upward force and the displacement of the tray is a horizontal displacement. As such, the angle between the force and the displacement is 90 degrees. If the work done by the waiter on the tray were to be calculated, then the results would be 0. Regardless of the magnitude of the force and displacement, F*d*cosine 90 degrees is 0 (since the cosine of 90 degrees is 0). A vertical force can never cause a horizontal displacement; thus, a vertical force does not do work on a horizontally displaced object!!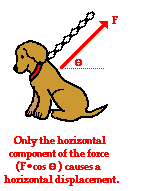
The equation for work lists three variables - each variable is associated with one of the three key words mentioned in the definition of work (force, displacement, and cause). The angle theta in the equation is associated with the amount of force that causes a displacement. As mentioned in a previous unit, when a force is exerted on an object at an angle to the horizontal, only a part of the force contributes to (or causes) a horizontal displacement. Let's consider the force of a chain pulling upwards and rightwards upon Fido in order to drag Fido to the right. It is only the horizontal component of the tension force in the chain that causes Fido to be displaced to the right. The horizontal component is found by multiplying the force F by the cosine of the angle between F and d. In this sense, the cosine theta in the work equation relates to the cause factor - it selects the portion of the force that actually causes a displacement.The Meaning of Theta
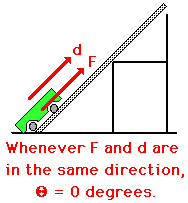When determining the measure of the angle in the work equation, it is important to recognize that the angle has a precise definition - it is the angle between the force and the displacement vector. Be sure to avoid mindlessly using any 'ole angle in the equation. A common physics lab involves applying a force to displace a cart up a ramp to the top of a chair or box. A force is applied to a cart to displace it up the incline at constant speed. Several incline angles are typically used; yet, the force is always applied parallel to the incline. The displacement of the cart is also parallel to the incline. Since F and d are in the same direction, the angle theta in the work equation is 0 degrees. Nevertheless, most students experienced the strong temptation to measure the angle of incline and use it in the equation. Don't forget: the angle in the equation is not just any 'ole angle. It is defined as the angle between the force and the displacement vector.
Which Path Requires the Most Energy?
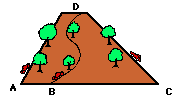Suppose that a car traveled up three different roadways (each with varying incline angle or slope) from the base of a mountain to the summit of the mountain. Which path would require the most gasoline (or energy)? Would the steepest path (path AD) require the most gasoline or would the least steep path (path BD) require the most gasoline? Or would each path require the same amount of gasoline?
This situation can be simulated by use of a simple physics lab in which a force is applied to raise a cart up an incline at constant speed to the top of a seat. Three different incline angles could be used to represent the three different paths up the mountain. The seat top represents the summit of the mountain. And the amount of gasoline (or energy) required to ascend from the base of the mountain to the summit of the mountain would be represented by the amount of work done on the cart to raise it from the floor to the seat top. The amount of work done to raise the cart from the floor to the seat top is dependent upon the force applied to the cart and the displacement caused by this force. Typical results of such a physics lab are depicted in the animation below.
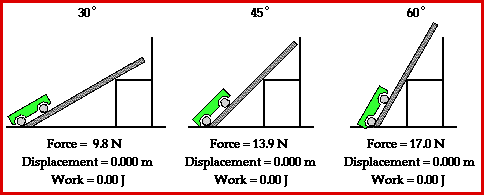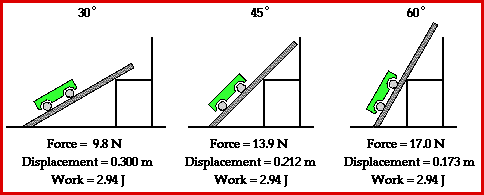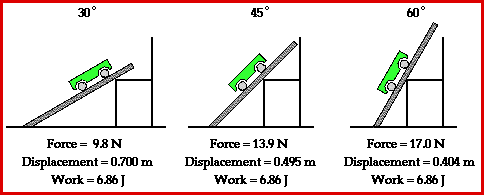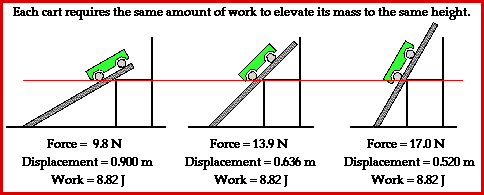
Observe in the animation that each path up to the seat top (representing the summit of the mountain) requires the same amount of work. The amount of work done by a force on any object is given by the equation
Work = F * d * cosine(Theta)
where F is the force, d is the displacement and Theta is the angle between the force and the displacement vector.
The least steep incline (30-degree incline angle) will require the least amount of force while the most steep incline will require the greatest amount of force. Yet, force is not the only variable affecting the amount of work done by the car in ascending to a certain elevation. Another variable is the displacement which is caused by this force. A look at the animation above reveals that the least steep incline would correspond to the largest displacement and the most steep incline would correspond to the smallest displacement. The final variable is Theta - the angle between the force and the displacement vector. Theta is 0-degrees in each situation. That is, the force is in the same direction as the displacement and thus makes a 0-degree angle with the displacement vector. So when the force is greatest (steep incline) the displacement is smallest and when the force is smallest (least steep incline) the displacement is largest. Subsequently, each path happens to require the same amount of work to elevate the object from the base to the same summit elevation.
Another perspective from which to analyze this situation is from the perspective of potential and kinetic energy and work. The work done by an external force (in this case, the force applied to the cart) changes the total mechanical energy of the object. In fact, the amount of work done by the applied force is equal to the total mechanical energy change of the object. The mechanical energy of the cart takes on two forms - kinetic energy and potential energy. In this situation, the cart was pulled at a constant speed from a low height to a high height. Since the speed was constant, the kinetic energy of the cart was not changed. Only the potential energy of the cart was changed. In each instance (30-degree, 45-degree, and 60-degree incline), the potential energy change of the cart was the same. The same cart was elevated from the same initial height to the same final height. If the potential energy change of each cart is the same, then the total mechanical energy change is the same for each cart. Finally, it can be reasoned that the work done on the cart must be the same for each path. On occasion, a force acts upon a moving object to hinder a displacement. Examples might include a car skidding to a stop on a roadway surface or a baseball runner sliding to a stop on the infield dirt. In such instances, the force acts in the direction opposite the objects motion in order to slow it down. The force doesn't cause the displacement but rather hinders it. These situations involve what is commonly called negative work. The negative of negative work refers to the numerical value that results when values of F, d and theta are substituted into the work equation. Since the force vector is directly opposite the displacement vector, theta is 180 degrees. The cosine(180 degrees) is -1 and so a negative value results for the amount of work done upon the object. Negative work will become important (and more meaningful) in Lesson 2 as we begin to discuss the relationship between work and energy. Whenever a new quantity is introduced in physics, the standard metric units associated with that quantity are discussed. In the case of work (and also energy), the standard metric unit is the Joule (abbreviated J). One Joule is equivalent to one Newton of force causing a displacement of one meter. In other words, In fact, any unit of force times any unit of displacement is equivalent to a unit of work. Some nonstandard units for work are shown below. Notice that when analyzed, each set of units is equivalent to a force unit times a displacement unit. In summary, work is done when a force acts upon an object to cause a displacement. Three quantities must be known in order to calculate the amount of work. Those three quantities are force, displacement and the angle between the force and the displacement.
The Meaning of Negative Work
Units of Work
Non-standard Units of Work:
foot•pound
kg•(m/s2)•m
kg•(m2/s2)