Analysis of Situations Involving External Forces
The previous part of Lesson 2 discussed the relationship between work and energy change. Whenever work is done upon an object by an external force, there will be a change in the total mechanical energy of the object. If only internal forces are doing work (no work done by external forces), there is no change in total mechanical energy; the total mechanical energy is said to be conserved. Because external forces are capable of changing the total mechanical energy of an object, they are sometimes referred to as nonconservative forces. Because internal forces do not change the total mechanical energy of an object, they are sometimes referred to as conservative forces. In this part of Lesson 2, we will further explore the quantitative relationship between work and energy.
Relating Work to Energy
The quantitative relationship between work and mechanical energy is expressed by the following equation:
The equation states that the initial amount of total mechanical energy (TMEi) plus the work done by external forces (Wext) is equal to the final amount of total mechanical energy (TMEf). A few notes should be made about the above equation. First, the mechanical energy can be either potential energy (in which case it could be due to springs or gravity) or kinetic energy. Given this fact, the above equation can be rewritten as
The second note that should be made about the above equation is that the work done by external forces can be a positive or a negative work term. Whether the work term takes on a positive or a negative value is dependent upon the angle between the force and the motion. Recall from Lesson 1 that the work is dependent upon the angle between the force and the displacement vectors. If the angle is 180 degrees as it occasionally is, then the work term will be negative. If the angle is 0 degrees, then the work term will be positive.
The above equation is expresses the quantitative relationship between work and energy. This equation will be the basis for the rest of this unit. It will form the basis of the conceptual aspect of our study of work and energy as well as the guiding force for our approach to solving mathematical problems. A large slice of the world of motion can be understood through the use of this relationship between work and energy.
Raising a Barbell Vertically
To begin our investigation of the work-energy relationship, we will investigate situations involving work being done by external forces (nonconservative forces). Consider a weightlifter who applies an upwards force (say 1000 N) to a barbell to displace it upwards a given distance (say 0.25 meters) at a constant speed. The initial energy plus the work done by the external force equals the final energy. If the barbell begins with 1500 Joules of energy (this is just a made up value) and the weightlifter does 250 Joules of work (F•d•cosine of angle = 1000 N•0.25 m•cosine 0 degrees = 250 J), then the barbell will finish with 1750 Joules of mechanical energy. The final amount of mechanical energy (1750 J) is equal to the initial amount of mechanical energy (1500 J) plus the work done by external forces (250 J).
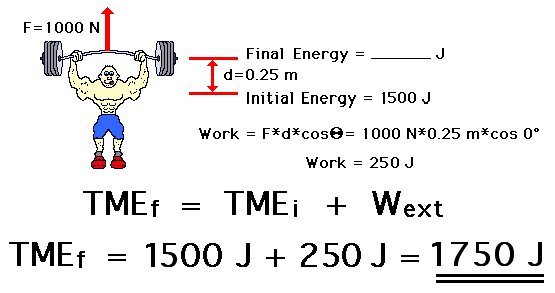
Catching a Baseball
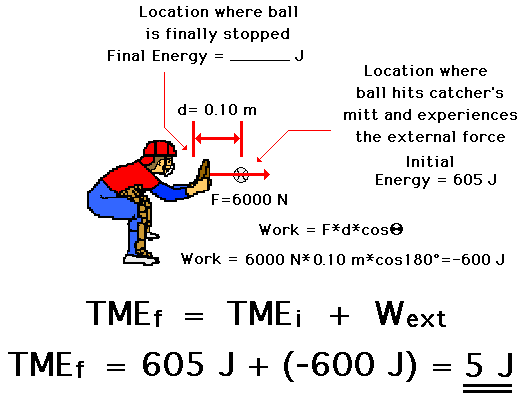
Now consider a baseball catcher who applies a rightward force (say 6000 N) to a leftward moving baseball to bring it from a high speed to a rest position over a given distance (say 0.10 meters). The initial energy plus the work done by the external force equals the final energy. If the ball begins with 605 Joules of energy (this is just another made up value), and the catcher does -600 Joules of work (F•d•cosine of angle = 6000 N•0.10 m•cosine 180 degrees = -600 J), then the ball will finish with 5 Joules of mechanical energy. The final energy (5 J) is equal to the initial energy (605 J) plus the work done by external forces (-600 J).
A Skidding Car
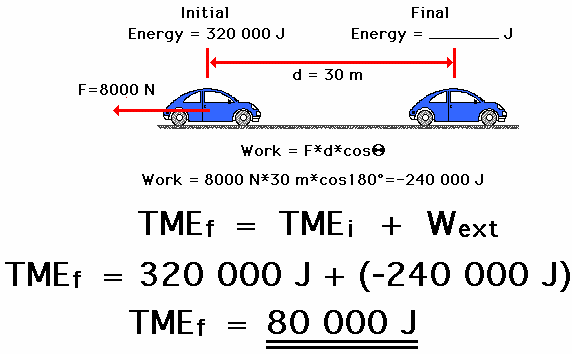
Now consider a car that is skidding from a high speed to a lower speed. The force of friction between the tires and the road exerts a leftward force (say 8000 N) on the rightward moving car over a given distance (say 30 m). The initial energy plus the work done by the external force equals the final energy. If the car begins with 320 000 Joules of energy (this is just another made up value), and the friction force does -240 000 Joules of work (F•d•cosine of angle = 8000 N•30 m•cosine 180 degrees = -240 000 J), then the car will finish with 80 000 Joules of mechanical energy. The final energy (80 000 J) is equal to the initial energy (320 000 J) plus the work done by external forces (-240 000 J).
ow Far Will It Skid?
Most driver's education classes teach future drivers that the stopping distance of a skidding car is directly proportional to the square of the speed of the car. That is a car traveling 10 mi/hr may require 4 feet to skid to an abrupt halt; but a car going twice as fast - 20 mi/hr - would require four times the distance - 16 feet to skid to a stop. A doubling of the speed results in a quadrupling of the stopping distance. A tripling of the speed would increase the stopping distance by a factor of nine. And a quadrupling of the speed would increase the stopping distance by a factor of 16. The stopping distance is proportional to the square of the speed of the vehicle.
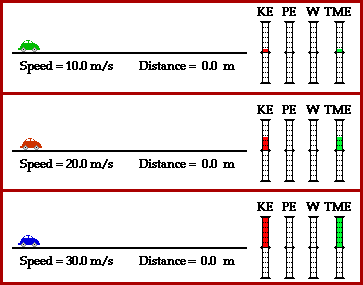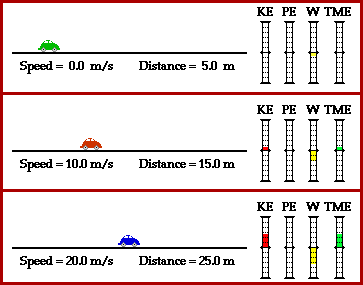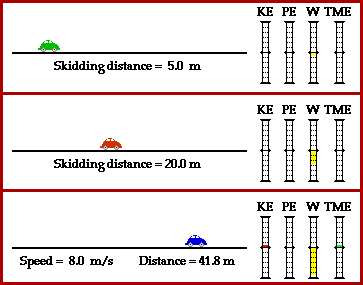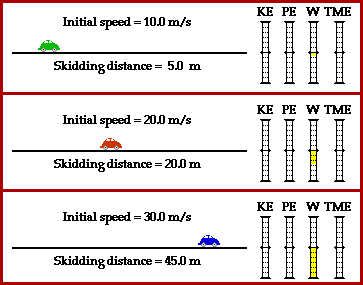
This mathematical relationship between initial speed and stopping distance is depicted in the animation below. Three cars with identical braking systems are traveling three different speeds. Prior to braking, the red car is traveling twice as fast as the green car (20 m/s is two times as big as 10 m/s); and prior to braking, the blue car is traveling three times as fast as the green car (30 m/s is three times as big as 10 m/s). The animation depicts that the stopping distance of the red car is four times (22) that of the green car and the stopping distance of the blue car is nine times (32) that of the green car.
Perhaps you learned in a drivers education course of this mathematical relationship between initial speed and stopping distance. But did you know that the relationship is based upon the physics of work and energy? Prior to braking each car has kinetic energy (energy due to motion). The amount of kinetic energy is dependent upon the mass and the speed of the car according to the equation
KE = 0/5*mass*(speed)2
The blue car has the most kinetic energy since it has the greatest speed. This is portrayed in the work-energy bar charts above by the height of the KE bar for each car.
Once the brakes are applied, the force of friction acts upon the car. The work done by friction on the skidding car is proportional to stopping distance according to the equation
Work = Force * displacement * cosine(Theta)
where the displacement of the car is simply the distance the car skids to a stop and Theta is the angle between the force and the displacement vectors. In this case, Theta is 180 degrees since the force of friction and the displacement of the car are in opposite directions.
The work done by friction on the car is related to the initial kinetic energy of the car. The work-energy relationship is often related by the equation
KEi + PEi + Wext = KEf + PEf
Since the potential energy of the car is the same in the initial state (before braking) as the final state (after stopping), each term can be canceled from the above equation. And since the car is finally stopped, the KEf term in the equation is zero. Thus, the equation becomes
0.5*m*v2 + F*d*cos(180) = 0.
This equation can be rearranged so that it takes the form of
0.5*m*v2 = -F*d*cos(180)
and since the cosine(180) is -1, the equation can be rewritten as
0.5*m*v2 = F*d.
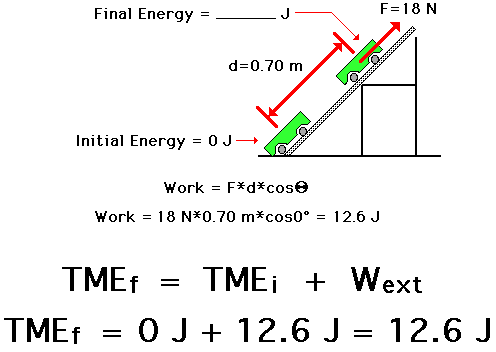
The above equation shows that the stopping distance (d) is proportional to the square of the speed (v2). And that's exactly what the driver's education course taught you. And now you know: it's PHYSICS! As a final example, consider a cart being pulled up an inclined plane at constant speed by a student during a Physics lab. The applied force on the cart (say 18 N) is directed parallel to the incline to cause the cart to be displaced parallel to the incline for a given displacement (say 0.7 m). The initial energy plus the work done by the external force equals the final energy. If the cart begins with 0 Joules of energy (this is just another made up value), and the student does 12.6 Joules of work (F•d•cosine of angle = 18 N•0.7 m•cosine 0 degrees = 12.6 J), then the cart will finish with 12.6 Joules of mechanical energy. The final energy (12.6 J) is equal to the initial energy (0 J) plus the work done by external forces (12.6 J).
Pulling a Cart Up an Incline at Constant Speed
Which Path Requires the Most Energy?
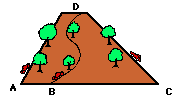Suppose that a car traveled up three different roadways (each with varying incline angle or slope) from the base of a mountain to the summit of the mountain. Which path would require the most gasoline (or energy)? Would the steepest path (path AD) require the most gasoline or would the least steep path (path BD) require the most gasoline? Or would each path require the same amount of gasoline?
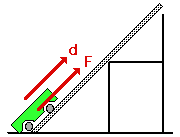This situation can be simulated by use of a simple physics lab in which a force is applied to raise a cart up an incline at constant speed to the top of a seat. Three different incline angles could be used to represent the three different paths up the mountain. The seat top represents the summit of the mountain. And the amount of gasoline (or energy) required to ascend from the base of the mountain to the summit of the mountain would be represented by the amount of work done on the cart to raise it from the floor to the seat top. The amount of work done to raise the cart from the floor to the seat top is dependent upon the force applied to the cart and the displacement caused by this force. Typical results of such a physics lab are depicted in the animation below.
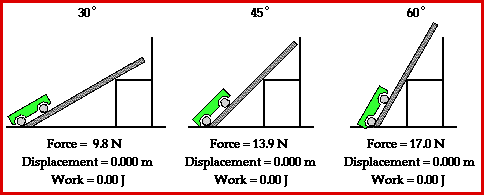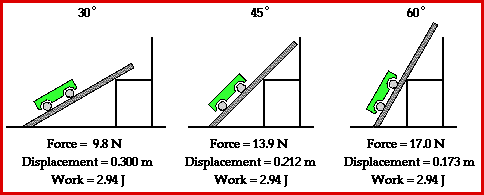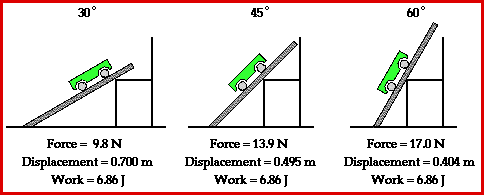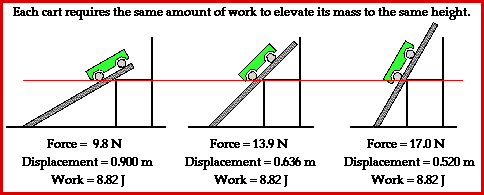
Observe in the animation that each path up to the seat top (representing the summit of the mountain) requires the same amount of work. The amount of work done by a force on any object is given by the equation
Work = F * d * cosine(Theta)
where F is the force, d is the displacement and Theta is the angle between the force and the displacement vector.
The least steep incline (30-degree incline angle) will require the least amount of force while the most steep incline will require the greatest amount of force. Yet, force is not the only variable affecting the amount of work done by the car in ascending to a certain elevation. Another variable is the displacement which is caused by this force. A look at the animation above reveals that the least steep incline would correspond to the largest displacement and the most steep incline would correspond to the smallest displacement. The final variable is Theta - the angle between the force and the displacement vector. Theta is 0-degrees in each situation. That is, the force is in the same direction as the displacement and thus makes a 0-degree angle with the displacement vector. So when the force is greatest (steep incline) the displacement is smallest and when the force is smallest (least steep incline) the displacement is largest. Subsequently, each path happens to require the same amount of work to elevate the object from the base to the same summit elevation.
Another perspective from which to analyze this situation is from the perspective of potential and kinetic energy and work. The work done by an external force (in this case, the force applied to the cart) changes the total mechanical energy of the object. In fact, the amount of work done by the applied force is equal to the total mechanical energy change of the object. The mechanical energy of the cart takes on two forms - kinetic energy and potential energy. In this situation, the cart was pulled at a constant speed from a low height to a high height. Since the speed was constant, the kinetic energy of the cart was not changed. Only the potential energy of the cart was changed. In each instance (30-degree, 45-degree, and 60-degree incline), the potential energy change of the cart was the same. The same cart was elevated from the same initial height to the same final height. If the potential energy change of each cart is the same, then the total mechanical energy change is the same for each cart. Finally, it can be reasoned that the work done on the cart must be the same for each path.
n each of these examples, an external force does work upon an object over a given distance to change the total mechanical energy of the object. If the external force (or nonconservative force) does positive work, then the object gains mechanical energy. The amount of energy gained is equal to the work done on the object. If the external force (or nonconservative force) does negative work, then the object loses mechanical energy. The amount of mechanical energy lost is equal to the work done on the object. In general, the total mechanical energy of the object in the initial state (prior to the work being done) plus the work done equals the total mechanical energy in the final state.
Your Turn to Try It
The work-energy relationship presented here can be combined with the expressions for potential and kinetic energy to solve complex problems. Like all complex problems, they can be made simple if first analyzed from a conceptual viewpoint and broken down into parts. In other words, avoid treating work-energy problems as mere mathematical problems. Rather, engage your mind and utilize your understanding of physics concepts to approach the problem. Ask "What forms of energy are present initially and finally?" and "Based on the equations, how much of each form of energy is present initially and finally?" and "Is work being done by external forces?" Use this approach on the following three practice problems. After solving, click the button to view the answers.
A 1000-kg car traveling with a speed of 25 m/s skids to a stop. The car experiences an 8000 N force of friction. Determine the stopping distance of the car.
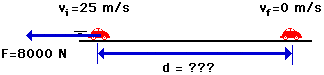
Initially:
PE = 0 J (the car's height is zero)KE = 0.5*1000*(25)^2 = 312 500 J
Finally:
PE = 0 J (the car's height is zero)KE = 0 J (the car's speed is zero)
The work done is (8000 N) • (d) • cos 180 = - 8000*d
Using the equation,
TMEi + Wext = TMEf312 500 J + (-8000 • d) = 0 J
Using some algebra it can be shown that d=39.1 m
At the end of the Shock Wave roller coaster ride, the 6000-kg train of cars (includes passengers) is slowed from a speed of 20 m/s to a speed of 5 m/s over a distance of 20 meters. Determine the braking force required to slow the train of cars by this amount.
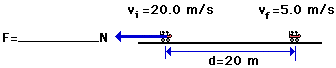
Initially:
PE = 0 J (the car's height is zero)KE = 0.5*6000*(20)^2 = 1 200 000 J
Finally:
PE = 0 J (the car's height is zero)KE = 0.5*6000*(5)^2 = 75 000 J
The work done is F • 20 • cos 180 = -20•F
Using the equation,
TMEi + Wext = TMEf1 200 000 J + (-20*F) = 75 000 J
Using some algebra, it can be shown that 20*F = 1 125 000 and so F = 56 250 N
A shopping cart full of groceries is sitting at the top of a 2.0-m hill. The cart begins to roll until it hits a stump at the bottom of the hill. Upon impact, a 0.25-kg can of peaches flies horizontally out of the shopping cart and hits a parked car with an average force of 500 N. How deep a dent is made in the car (i.e., over what distance does the 500 N force act upon the can of peaches before bringing it to a stop)?
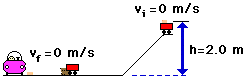
The question pertains to the can of peaches; so focus on the can (not the cart).
Initially:
PE = 0.25 kg * 9.8 m/s/s * 2 m = 4.9 JKE = 0 J (the peach can is at rest)
Finally:
PE = 0 J (the can's height is zero)KE = 0 J (the peach can is at rest)
The work done is 500 N*d*cos 180 = -500*d
Using the equation,
TMEi + Wext = TMEf4.9 J + (-500*d) = 0 J
Using some algebra, it can be shown that d = 0.0098 m (9.8 mm)
All three of the above problems have one thing in common: there is a force that does work over a distance in order to remove mechanical energy from an object. The force acts opposite the object's motion (angle between force and displacement is 180 degrees) and thus does negative work. Negative work results in a loss of the object's total amount of mechanical energy. In each situation, the work is related to the kinetic energy change. And since the distance (d) over which the force does work is related to the work and since the velocity squared (v^2) of the object is related to the kinetic energy, there must also be a direct relation between the stopping distance and the velocity squared. Observe the derivation below. KEi + Wext = 0 J 0.5•m•vi2 + F•d•cos(Theta) = 0 J 0.5•m•vi2 = F•d vi2 The above equation depicts stopping distance as being dependent upon the square of the velocity. This means that a twofold increase in velocity would result in a fourfold (two squared) increase in stopping distance. A threefold increase in velocity would result in a nine-fold (three squared) increase in stopping distance. And a fourfold increase in velocity would result in a sixteen-fold (four squared) increase in stopping distance. This is one more example in which an equation becomes more than a mere algebraic recipe for solving problems. Equations can also be powerful guides to thinking about how two quantities are related to each other. In the case of a horizontal force bringing an object to a stop over some horizontal distance, the stopping distance of the object is related to the square of the velocity of the object. d = 16 m From 5 m/s to 10 m/s is a two-fold increase (10 / 5 = 2) in velocity. Thus there should be a four-fold increase in stopping distance. Multiply 4 m by 4. d = 36 m From 5 m/s to 15 m/s is a three-fold increase (15 / 5 = 3) in velocity. Thus there should be a nine-fold increase in stopping distance. Multiply 4 m by 9. d = 64 m From 5 m/s to 20 m/s is a four-fold increase (20 / 5 = 4) in velocity. Thus there should be a 16-fold increase in stopping distance. Multiply 4 m by 16. d = 100 m From 5 m/s to 25 m/s is a five-fold increase (25 / 5 = 5) in velocity. Thus, there should be a 25-fold increase in stopping distance. Multiply 4 m by 25. The above principle - that stopping distance is proportional to velocity squared - is often the focus of a popular physics lab. A Hot wheels car is rolled down an inclined plane to the floor below. Once reaching the floor, it strikes a computer diskette box and skids to a stop as a result of the friction between the car/box system and the floor. A photo gate time is used to determine the speed of the car prior to striking the box. Several trials are performed and a data set is collected and plotted. As the speed of the car is increased, the stopping distance is increased. If the data are plotted, then a clear power relationship is seen. If power regression is performed on the data set, the results tend to show that d = k•v2 where k is a constant of proportionality.
Stopping Distance
d
Test your understanding by predicting the stopping distance values in the table below (and see the practice problems at the end of this page).
The examples mentioned on this page involve the application of the work-energy relationship to situations involving external or nonconservative forces doing work. An entirely different outcome results in situations in which there is no work done by external forces. The next part of Lesson 2 involves an analysis of these situations.