We all have a feel for what temperature is. We even have a shared language that we use to qualitatively describe temperature. The water in the shower or bathtub feels hot or cold or warm. The weather outside is chilly or steamy. We certainly have a good feel for how one temperature is qualitatively different than another temperature. We may not always agree on whether the room temperature is too hot or too cold or just right. But we will likely all agree that we possess built-in thermometers for making qualitative judgments about relative temperatures.
 

What is Temperature?

Despite our built-in feel for temperature, it remains one of those concepts in science that is difficult to define. It seems that a tutorial page exploring the topic of temperature and thermometers should begin with a simple definition of temperature. But it is at this point that I'm stumped. So I turn to that familiar resource, Dictionary.com ... where I find definitions that vary from the simple-yet-not-too-enlightening to the too-complex-to-be-enlightening. At the risk of doing a belly flop in the pool of enlightenment, I will list some of those definitions here:

• The degree of hotness or coldness of a body or environment.
• A measure of the warmth or coldness of an object or substance with reference to some standard value.
• A measure of the average kinetic energy of the particles in a sample of matter, expressed in terms of units or degrees designated on a standard scale.
• A measure of the ability of a substance, or more generally of any physical system, to transfer heat energy to another physical system.
• Any of various standardized numerical measures of this ability, such as the Kelvin, Fahrenheit, and Celsius scale.

For certain, we are comfortable with the first two definitions - the degree or measure of how hot or cold an object is. But our understanding of temperature is not furthered by such definitions. The third and the fourth definitions that reference the kinetic energy of particles and the ability of a substance to transfer heat are scientifically accurate. However, these definitions are far too sophisticated to serve as good starting points for a discussion of temperature. So we will resign to a definition similar to the fifth one that is listed - temperature can be defined as the reading on a thermometer. Admittedly, this definition lacks the power that is needed for eliciting the much-desired Aha! Now I Understand! moment. Nonetheless it serves as a great starting point for this lesson on heat and temperature. Temperature is what the thermometer reads. Whatever it is that temperature is a measure of, it is reflected by the reading on a thermometer. So exactly how does a thermometer work? How does it reliably meter whatever it is that temperature is a measure of?
 

How a Thermometer Works

Today, there are a variety of types of thermometers. The type that most of us are familiar with from science class is the type that consists of a liquid encased in a narrow glass column. Older thermometers of this type used liquid mercury. In response to our understanding of the health concerns associated with mercury exposure, these types of thermometers usually use some type of liquid alcohol. These liquid thermometers are based on the principal of thermal expansion. When a substance gets hotter, it expands to a greater volume. Nearly all substances exhibit this behavior of thermal expansion. It is the basis of the design and operation of thermometers.

As the temperature of the liquid in a thermometer increases, its volume increases. The liquid is enclosed in a tall, narrow glass (or plastic) column with a constant cross-sectional area. The increase in volume is thus due to a change in height of the liquid within the column. The increase in volume, and thus in the height of the liquid column, is proportional to the increase in temperature. Suppose that a 10-degree increase in temperature causes a 1-cm increase in the column's height. Then a 20-degree increase in temperature will cause a 2-cm increase in the column's height. And a 30-degree increase in temperature will cause s 3-cm increase in the column's height. The relationship between the temperature and the column's height is linear over the small temperature range for which the thermometer is used. This linear relationship makes the calibration of a thermometer a relatively easy task.

The calibration of any measuring tool involves the placement of divisions or marks upon the tool to measure a quantity accurately in comparison to known standards. Any measuring tool - even a meter stick - must be calibrated. The tool needs divisions or markings; for instance, a meter stick typically has markings every 1-cm apart or every 1-mm apart. These markings must be accurately placed and the accuracy of their placement can only be judged when comparing it to another object that is precisely known to have a certain length.

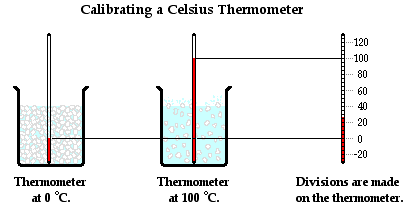
A thermometer is calibrated by using two objects of known temperatures. The typical process involves using the freezing point and the boiling point of pure water. Water is known to freeze at 0°C and to boil at 100°C at an atmospheric pressure of 1 atm. By placing a thermometer in mixture of ice water and allowing the thermometer liquid to reach a stable height, the 0-degree mark can be placed upon the thermometer. Similarly, by placing the thermometer in boiling water (at 1 atm of pressure) and allowing the liquid level to reach a stable height, the 100-degree mark can be placed upon the thermometer. With these two markings placed upon the thermometer, 100 equally spaced divisions can be placed between them to represent the 1-degree marks. Since there is a linear relationship between the temperature and the height of the liquid, the divisions between 0 degree and 100 degree can be equally spaced. With a calibrated thermometer, accurate measurements can be made of the temperature of any object within the temperature range for which it has been calibrated.

Temperature Scales

The thermometer calibration process described above results in what is known as a centigrade thermometer. A centigrade thermometer has 100 divisions or intervals between the normal freezing point and the normal boiling point of water. Today, the centigrade scale is known as the Celsius scale, named after the Swedish astronomer Anders Celsius who is credited with its development. The Celsius scale is the most widely accepted temperature scale used throughout the world. It is the standard unit of temperature measurement in nearly all countries, the most notable exception being the United States. Using this scale, a temperature of 28 degrees Celsius is abbreviated as 28°C.

Traditionally slow to adopt the metric system and other accepted units of measurements, the United States more commonly uses the Fahrenheit temperature scale. A thermometer can be calibrated using the Fahrenheit scale in a similar manner as was described above. The difference is that the normal freezing point of water is designated as 32 degrees and the normal boiling point of water is designated as 212 degrees in the Fahrenheit scale. As such, there are 180 divisions or intervals between these two temperatures when using the Fahrenheit scale. The Fahrenheit scale is named in honor of German physicist Daniel Fahrenheit. A temperature of 76 degree Fahrenheit is abbreviated as 76°F. In most countries throughout the world, the Fahrenheit scale has been replaced by the use of the Celsius scale.

Temperatures expressed by the Fahrenheit scale can be converted to the Celsius scale equivalent using the equation below:

°C = (°F - 32°)/1.8

Similarly, temperatures expressed by the Celsius scale can be converted to the Fahrenheit scale equivalent using the equation below:

°F= 1.8•°C + 32°

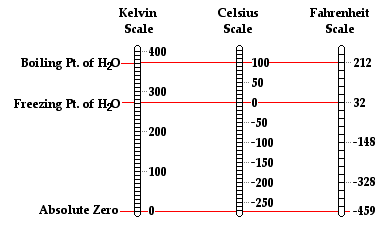
The Kelvin Temperature Scale

While the Celsius and Fahrenheit scales are the most widely used temperature scales, there are several other scales that have been used throughout history. For example, there is the Rankine scale, the Newton scale and the Romer scale, all of which are rarely used. Finally, there is the Kelvin temperature scale, which is the standard metric system of temperature measurement and perhaps the most widely used temperature scale among scientists. The Kelvin temperature scale is similar to the Celsius temperature scale in the sense that there are 100 equal degree increments between the normal freezing point and the normal boiling point of water. However, the zero-degree mark on the Kelvin temperature scale is 273.15 units cooler than it is on the Celsius scale. So a temperature of 0 Kelvin is equivalent to a temperature of -273.15 °C. Observe that the degree symbol is not used with this system. So a temperature of 300 units above 0 Kelvin is referred to as 300 Kelvin and not 300 degree Kelvin; such a temperature is abbreviated as 300 K. Conversions between Celsius temperatures and Kelvin temperatures (and vice versa) can be performed using one of the two equations below.

°C = K - 273.15°

K = °C + 273.15

The zero point on the Kelvin scale is known as absolute zero. It is the lowest temperature that can be achieved. The concept of an absolute temperature minimum was promoted by Scottish physicist William Thomson (a.k.a. Lord Kelvin) in 1848. Thomson theorized based on thermodynamic principles that the lowest temperature which could be achieved was -273°C. Prior to Thomson, experimentalists such as Robert Boyle (late 17th century) were well aware of the observation that the volume (and even the pressure) of a sample of gas was dependent upon its temperature. Measurements of the variations of pressure and volume with changes in the temperature could be made and plotted. Plots of volume vs. temperature (at constant pressure) and pressure vs. temperature (at constant volume) reflected the same conclusion - the volume and the pressure of a gas reduces to zero at a temperature of -273°C. Since these are the lowest values of volume and pressure that are possible, it is reasonable to conclude that -273°C was the lowest temperature that was possible.

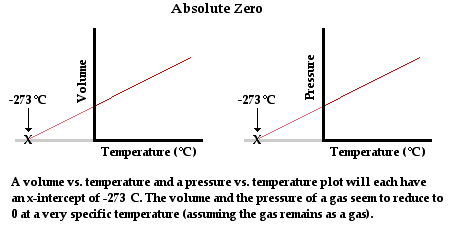
Thomson referred to this minimum lowest temperature as absolute zero and argued that a temperature scale be adopted that had absolute zero as the lowest value on the scale. Today, that temperature scale bears his name. Scientists and engineers have been able to cool matter down to temperatures close to -273.15°C, but never below it. In the process of cooling matter to temperatures close to absolute zero, a variety of unusual properties have been observed. These properties include superconductivity, superfluidity and a state of matter known as a Bose-Einstein condensate.

Temperature is what the thermometer reads. But what exactly is temperature a reflection of? The concept of an absolute zero temperature is quite interesting and the observation of remarkable physical properties for samples of matter approaching absolute zero makes one ponder the topic more deeply. Is there something happening at the particle level which is related to the observations made at the macroscopic level? Is there something deeper to temperature than simply the reading on a thermometer? As the temperature of a sample of matter increases or decreases, what is happening at the level of atoms and molecules? These questions will be addressed on the next page of Lesson 1.