Analysis of Situations in Which Mechanical Energy is Conserved
t has previously been mentioned that there is a relationship between work and mechanical energy change. Whenever work is done upon an object by an external force (or nonconservative force), there will be a change in the total mechanical energy of the object. If only internal forces are doing work (no work done by external forces), then there is no change in the total amount of mechanical energy. The total mechanical energy is said to be conserved. In this part of Lesson 2, we will further explore the quantitative relationship between work and mechanical energy in situations in which there are no external forces doing work.
The quantitative relationship between work and the two forms of mechanical energy is expressed by the following equation:
The equation illustrates that the total mechanical energy (KE + PE) of the object is changed as a result of work done by external forces. There are a host of other situations in which the only forces doing work are internal or conservative forces. In such situations, the total mechanical energy of the object is not changed. The external work term cancels from the above equation and mechanical energy is conserved. The previous equation is simplified to the following form:
In these situations, the sum of the kinetic and potential energy is everywhere the same. As the potential energy is increased due to the stretch/compression of a spring or an increase in its height above the earth, the kinetic energy is decreased due to the object slowing down. As the potential energy is decreased due to the return of a spring to its rest position or a decrease in height above the earth, the kinetic energy is increased due to the object speeding up. We would say that energy is transformed or changes its form from kinetic energy to potential energy (or vice versa); yet the total amount present is conserved - i.e., always the same.
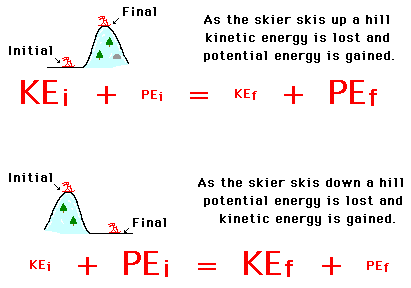
The Example of Pendulum Motion
 The tendency of an object to conserve its mechanical energy is observed whenever external forces are not doing any overall work. If the influence of friction and air resistance can be ignored (or assumed to be negligible) and all other external forces are absent or merely not doing work, then the object is often said to conserve its energy. Consider a pendulum bob swinging to and fro on the end of a string. There are only two forces acting upon the pendulum bob. Gravity (an internal force) acts downward and the tensional force (an external force) pulls upwards towards the pivot point. The external force does not do work since at all times it is directed at a 90-degree angle to the motion. (Review a previous page to convince yourself that F•d•cosine angle = 0 J for the force of tension.)
The tendency of an object to conserve its mechanical energy is observed whenever external forces are not doing any overall work. If the influence of friction and air resistance can be ignored (or assumed to be negligible) and all other external forces are absent or merely not doing work, then the object is often said to conserve its energy. Consider a pendulum bob swinging to and fro on the end of a string. There are only two forces acting upon the pendulum bob. Gravity (an internal force) acts downward and the tensional force (an external force) pulls upwards towards the pivot point. The external force does not do work since at all times it is directed at a 90-degree angle to the motion. (Review a previous page to convince yourself that F•d•cosine angle = 0 J for the force of tension.)
As the pendulum bob swings to and fro, its height above the tabletop (and in turn its speed) is constantly changing. As the height decreases, potential energy is lost; and simultaneously the kinetic energy is gained. Yet at all times, the sum of the potential and kinetic energies of the bob remains constant. The total mechanical energy is 6 J. There is no loss or gain of mechanical energy, only a transformation from kinetic energy to potential energy (and vice versa). This is depicted in the diagram below.
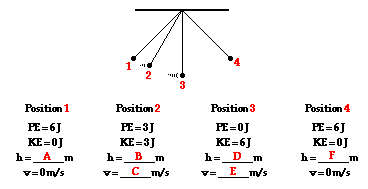
![]() As the 2.0-kg pendulum bob in the above diagram swings to and fro, its height and speed change. Use energy equations and the above data to determine the blanks in the above diagram. Click the button to view answers.
As the 2.0-kg pendulum bob in the above diagram swings to and fro, its height and speed change. Use energy equations and the above data to determine the blanks in the above diagram. Click the button to view answers.
A: h = 0.306 m (6 J = 2 kg *9.8 m/s/s * h)
B: h = 0.153 m (3 J = 2 kg *9.8 m/s/s * h)
C: v = 1.73 m/s (3 J = 0.5 * 2 kg * v2)
D: h = 0 m (0 J = 2 kg * 9.8 m/s/s*h)
E: v = 2.45 m/s (6 J = 0.5 * 2 kg * v2)
F: h = 0.306 m (6 J = 2 kg * 9.8 m/s/s * h) A common Physics lab involves the analysis of a pendulum in its back and forth motion. The transformation and conservation of mechanical energy is the focus of the lab.
Learning From Lab
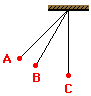 A 0.200-kg (200 gram) pendulum is typically released from rest at location A. The bob passes through a photogate at location B and another photogate at location C. The speed of the pendulum bob can be determined from the width of the bob and the photogate times. The speed and mass can be used to determine the kinetic energy of the bob at each of the three locations. The heights of the bob above the tabletop at each of the three locations can be measured and used to determine the potential energy of the bob. The data should reflect that the mechanical energy changes its form as the bob passes from location A to B to C. Yet the total mechanical energy should remain relativity constant. Sample data for such a lab are shown below.
A 0.200-kg (200 gram) pendulum is typically released from rest at location A. The bob passes through a photogate at location B and another photogate at location C. The speed of the pendulum bob can be determined from the width of the bob and the photogate times. The speed and mass can be used to determine the kinetic energy of the bob at each of the three locations. The heights of the bob above the tabletop at each of the three locations can be measured and used to determine the potential energy of the bob. The data should reflect that the mechanical energy changes its form as the bob passes from location A to B to C. Yet the total mechanical energy should remain relativity constant. Sample data for such a lab are shown below.
The sample data show that the pendulum bob loses potential energy as it swings from the more elevated location at A to the lower location at B and at C. As this loss of potential energy occurs, the pendulum bob gains kinetic energy. Yet the total mechanical energy remains approximately 0.785 Joules. We would say that total mechanical energy is conserved as the potential energy is transformed into kinetic energy.
Energy Transformation for a Pendulum
The motion of a pendulum is a classic example of mechanical energy conservation. A pendulum consists of a mass (known as a bob) attached by a string to a pivot point. As the pendulum moves it sweeps out a circular arc, moving back and forth in a periodic fashion. Neglecting air resistance (which would indeed be small for an aerodynamically shaped bob), there are only two forces acting upon the pendulum bob. One force is gravity. The force of gravity acts in a downward direction and does work upon the pendulum bob. However, gravity is an internal force (or conservative force) and thus does not serve to change the total amount of mechanical energy of the bob. The other force acting upon the bob is the force of tension. Tension is an external force and if it did do work upon the pendulum bob it would indeed serve to change the total mechanical energy of the bob. However, the force of tension does not do work since it always acts in a direction perpendicular to the motion of the bob. At all points in the trajectory of the pendulum bob, the angle between the force of tension and its direction of motion is 90 degrees. Thus, the force of tension does not do work upon the bob.
Since there are no external forces doing work, the total mechanical energy of the pendulum bob is conserved. The conservation of mechanical energy is demonstrated in the animation below. Observe the KE and PE bars of the bar chart; their sum is a constant value.
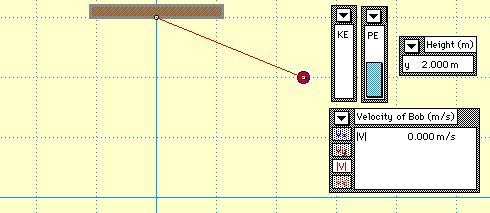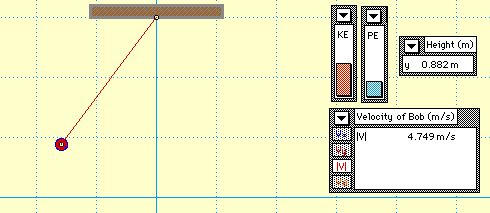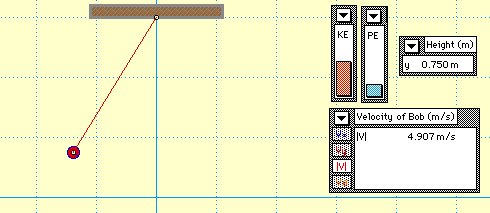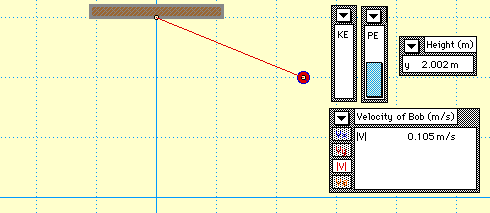
Observe that the falling motion of the bob is accompanied by an increase in speed. As the bob loses height and PE, it gains speed and KE; yet the total of the two forms of mechanical energy is conserved.
To test you understanding of the conservation principle, use the heights and the speeds given in the table below to fill in the remaining cells at the various locations in a 0.200-kg bob's trajectory. Use the pull down menus to check your work.
(Note: mass = 0.200 kg)
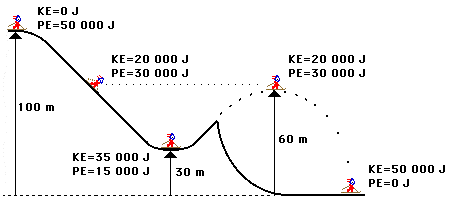
A roller coaster operates on this same principle of energy transformation. Work is initially done on a roller coaster car to lift to its initial summit. Once lifted to the top of the summit, the roller coaster car has a large quantity of potential energy and virtually no kinetic energy (the car is almost at rest). If it can be assumed that no external forces are doing work upon the car as it travels from the initial summit to the end of the track (where finally an external braking system is employed), then the total mechanical energy of the roller coaster car is conserved. As the car descends hills and loops, its potential energy is transformed into kinetic energy as the car speeds up. As the car climbs up hills and loops, its kinetic energy is transformed into potential energy as the car slows down. Yet in the absence of external forces doing work, the total mechanical energy of the car is conserved. Conservation of energy on a roller coaster ride means that the total amount of mechanical energy is the same at every location along the track. The amount of kinetic energy and the amount of potential energy is constantly changing. Yet the sum of the kinetic and potential energies is everywhere the same. This is illustrated in the diagram below. The total mechanical energy of the roller coaster car is a constant value of 40 000 Joules.
The Example of a Roller Coaster

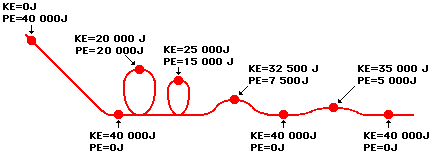
Energy Transformation on a Roller Coaster
A roller coaster ride is a thrilling experience which involves a wealth of physics. Part of the physics of a roller coaster is the physics of work and energy. The ride often begins as a chain and motor (or other mechanical device) exerts a force on the train of cars to lift the train to the top of a vary tall hill. Once the cars are lifted to the top of the hill, gravity takes over and the remainder of the ride is an experience in energy transformation.
At the top of the hill, the cars possess a large quantity of potential energy. Potential energy - the energy of vertical position - is dependent upon the mass of the object and the height of the object. The car's large quantity of potential energy is due to the fact that they are elevated to a large height above the ground. As the cars descend the first drop they lose much of this potential energy in accord with their loss of height. The cars subsequently gain kinetic energy. Kinetic energy - the energy of motion - is dependent upon the mass of the object and the speed of the object. The train of coaster cars speeds up as they lose height. Thus, their original potential energy (due to their large height) is transformed into kinetic energy (revealed by their high speeds). As the ride continues, the train of cars are continuously losing and gaining height. Each gain in height corresponds to the loss of speed as kinetic energy (due to speed) is transformed into potential energy (due to height). Each loss in height corresponds to a gain of speed as potential energy (due to height) is transformed into kinetic energy (due to speed). This transformation of mechanical energy from the form of potential to the form of kinetic and vice versa is illustrated in the animation below.
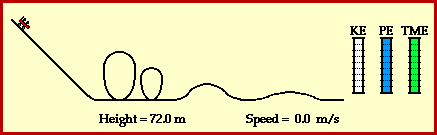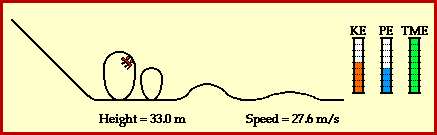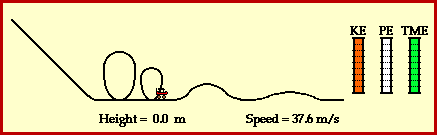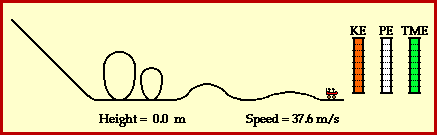
A roller coaster ride also illustrates the work and energy relationship. The work done by external forces is capable of changing the total amount of mechanical energy from an initial value to some final value. The amount of work done by the external forces upon the object is equal to the amount of change in the total mechanical energy of the object. The relationship is often stated in the form of the following mathematical equation.
KEinitial + PEinitial + Wexternal = KEfinal + PEfinal
The left side of the equation includes the total mechanical energy (KEinitial + PEinitial) for the initial state of the object plus the work done on the object by external forces (Wexternal) while the right side of the equation includes the total mechanical energy (KEfinal + PEfinal) for the final state of the object.
Once a roller coaster has reached its initial summit and begins its descent through loops, turns and smaller hills, the only forces acting upon the coaster cars are the force of gravity, the normal force and dissipative forces such as air resistance. The force of gravity is an internal force and thus any work done by it does not change the total mechanical energy of the train of cars. The normal force of the track pushing up on the cars is an external force. However, it is at all times directed perpendicular to the motion of the cars and thus is incapable of doing any work upon the train of cars. Finally, the air resistance force is capable of doing work upon the cars and thus draining a small amount of energy from the total mechanical energy which the cars possess. However, due to the complexity of this force and its small contribution to the large quantity of energy possessed by the cars, it is often neglected. By neglecting the influence of air resistance, it can be said that the total mechanical energy of the train of cars is conserved during the ride. That is to say, the total amount of mechanical energy (kinetic plus potential) possessed by the cars is the same throughout the ride. Energy is neither gained nor lost, only transformed from kinetic energy to potential energy and vice versa. The motion of a ski jumper is also governed by the transformation of energy. As a ski jumper glides down the hill towards the jump ramp and off the jump ramp towards the ground, potential energy is transformed into kinetic energy. If it can be assumed that no external forces are doing work upon the ski jumper as it travels from the top of the hill to the completion of the jump, then the total mechanical energy of the ski jumper is conserved. Consider Li Ping Phar, the esteemed Chinese ski jumper. She starts at rest on top of a 100-meter hill, skis down the 45-degree incline and makes a world record setting jump. Assuming that friction and air resistance have a negligible affect upon Li's motion and assuming that Li never uses her poles for propulsion, her total mechanical energy would never change. Of course it should be noted that the original assumption that was made for both the roller coaster car and the ski jumper is that there were no external forces doing work. In actuality, there are external forces doing work. Both the roller coaster car and the ski jumper experience the force of friction and the force of air resistance during the course of their motion. Friction and air resistance are both external forces and would do work upon the moving object. In fact, the presence of friction and air resistance would do negative work and cause the total mechanical energy to decrease during the course of the motion. While the assumption that mechanical energy is conserved is an invalid assumption, it is a useful approximation that assists in the analysis of an otherwise complex motion.
The Example of a Ski Jumper